At The Limit

Figure #1, Note, you can
imagine that a person
represents any number
of real people

Let's imagine the ultimate limit that the planet can keep alive at one time. The best technology that results in the most efficient techniques, regardless of sustainability, will be used to extract sustenance and that sustenance will be distributed as evenly as possible. None will be wasted. At that limit, the number of people cannot increase. Each birth must be offset by a death. We don't know what that number is, but to illustrate what happens, imagine the environment can keep 16 people alive at one time. Imagine that these 16 people are spread over four generations. There are four children, four parents, four grand parents, and four great grandparents. Each generation is separated by 25 years, because the parents create their children when they are 25. (see figure #1). The four great grandparents die of old age right before their great grandchildren give birth to the next generation, when they are almost 100 years old. If the new parents create two offspring for each (each parent counts their own children, which means each child will be counted twice; once by the mother and once by the father), this situation can go forever.

If the new parents create three children, then there will be 18 people alive, and that means there are two extra people than the environment can provide for. Two must die. The parents of these new children will certainly be stronger and more capable than the new great grandparents that just turned 75, so two of those great grandparents will die at the age of 75. Two will be able to live to old age of 100.

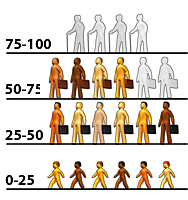
Figure #2

Now consider what happens if the next generation of parents resume producing two children each. These new parents will number 6, so they will produce 6 total children, and that means that all four great grandparents will die at 75. The next generation will bring in another set of 6 children, and that will cause not only all four new great grandparents to die at 75, it will cause two of the new grandparents to die at 50. This situation can go on forever, but notice that the birth of two extra children once in the history of this world, permanently reduced the average life expectancy from 100 down to 66 (see figure #2).

If each successive generation produces three children each. The next generation will produce nine babies, and thus all but one of the new grand parents will die at age 50. Only one will live to 75. When those nine babies grow up, they will bring 13.5 children into the world, but to keep this simple, we will round that down to 13. With 13 new mouths to feed and only 16 servings to go around, it is not obvious who is going to die, but we can take the extreme situation where all the children survive. This means only three parents will live, and thus three parents will provide for 13 children. When those 13 children reach adulthood, they will produce at least 19 children. That means that all 13 new parents and the 3 new grand parents will die, and three of the new born children will die. There will be 16 children and no adults. When those 16 reach 25, they will produce 24 children, and 8 will die, leaving 16. This can continue forever, which means that if the people average 3 children per person, then one in three children will die.

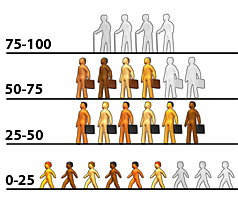
Figure #3

Of course it is absurd to think that 16 infants can provide for themselves, so we will consider a more rational case where we ensure approximately three adults for two children. This will end up in the steady state where there are six parents, four grandparents and six children. When those six children produce their nine babies, three babies will die, and again we see that if the society averages three children per person (see figure #3), then one in three die.

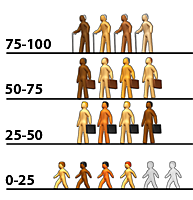
Figure #4

Consider the situation where the children die instead of an adult, so that all adults will die of old age at 100. In that case each generation will produce six babies and two of those babies will die. Again, if the population averages three children each (see figure #4), then one in three children will die.

This shows that at the limit, and if that limit remains stationary, and society averages more than 2 children, and attempts to keep more than an average of 2 alive, they will not succeed. By attempting this, the life expectancy of the adults will drop to some miserable level, more absolute numbers of children will die, and the death rate of children will still be determined by how many we average above two. The death rate of children will be (x-2)/x where x is the number of babies above 2 that adults create.

If the limit grows, then more than an average of 2 children can be kept and if the limit is shrinking, then less than 2 can be kept alive, proportional to how fast the limit is growing or shrinking.

The current population of humans on Earth is above what can be sustained, but at the limit of how many can be provided for. Resources that are necessary to provide for our numbers are being consumed faster than they renew, which means that this cannot be sustained.

It is hard to believe that one more person cannot be included without killing another, so it is difficult for many people to agree with "no more can be added". The Earth is a finite size, so there is a limit. We don't know what that limit is and it depends on our skills at getting the things we need to survive, but regardless, the limit is still there. There are many factors that determine the limit, so the limit is never a constant value.

This model shows how the population must behave at the limit, and when we comprehend how it must behave, we can make sense of what is happening in our world.

To find the "average number of children" ask all adults right before they die, how many children they created and survived, and average that number. Every child will be counted twice, once by the mother and once by the father. This number is very similar to the Total Fertility Rate

StopAtTwo has created the phrase "average number of children" because there are no other definitions or phrases that are adequate. Demographers have several different definitions to measure the birth rate more precicely, but none are quite what is needed.

  • Total Fertility Rate while this is nearly the correct definition, it is not something that most people are going to relate to. Demographers created it in order to be able to do their work.
  • Birth rate is used by demographers for measuring births per 1000 people, so this is not the right phrase.
  • Average number of children per person can be interpreted to mean that we sum the total number of people and divide by the number of children which is clearly not right.

To find the "average number of children" ask all adults right before they die, how many children they created and survived, and average that number. Every child will be counted twice, once by the mother and once by the father. This number is very similar to the Total Fertility Rate

StopAtTwo has created the phrase "average number of children" because there are no other definitions or phrases that are adequate. Demographers have several different definitions to measure the birth rate more precicely, but none are quite what is needed.

  • Total Fertility Rate while this is nearly the correct definition, it is not something that most people are going to relate to. Demographers created it in order to be able to do their work.
  • Birth rate is used by demographers for measuring births per 1000 people, so this is not the right phrase.
  • Average number of children per person can be interpreted to mean that we sum the total number of people and divide by the number of children which is clearly not right.